本文共 5787 字,大约阅读时间需要 19 分钟。
参考博文:https://blog.csdn.net/u012740992/article/details/89397714
论文文档:http://gamma.cs.unc.edu/ORCA/文章目录
1.问题定义
用简单的圆形或凸多边形代表机器
可被观察到的属性:- 设机器A是圆形,半径 r A r_A rA
- 机器位置 p A p_A pA
- 当前速度 v A v_A vA
观察不到的属性:
- 最大速度 v m a x v^{max} vmax
- 首选速度 V p r e f V^{pref} Vpref(大小等于最大速度,方向指向目标位置)
计算新速度 v n e w v^{new} vnew
- 保证所有机器在时间 τ \tau τ内不碰撞
- 新速度尽可能的接近 V p r e f V^{pref} Vpref
2. 速度障碍区 V O A ∣ B τ VO_{A|B}^{\tau} VOA∣Bτ(velocity obstacle)
有机器AB
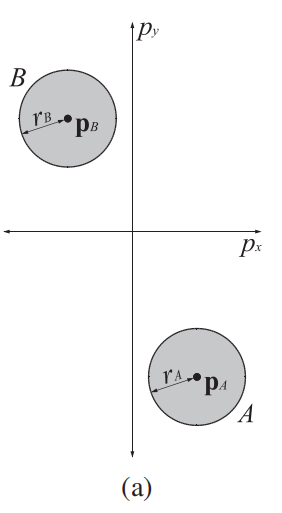
速度障碍区 V O A ∣ B τ VO_{A|B}^{\tau} VOA∣Bτ
- 把A化作质点,B可以当做半径 r A + r B r_A + r_B rA+rB的圆
- B相对A的位置 p B − p A p_B - p_A pB−pA
- A相对B的速度 v r = v A − v B v_r = v_A - v_B vr=vA−vB
- 如果A与B的相对速度 v A − v B v_A - v_B vA−vB在障碍速度 V O A ∣ B τ VO_{A|B}^{\tau} VOA∣Bτ范围内,在时间 τ \tau τ内,AB一定会碰撞 V O A ∣ B τ = { v ∣ ∃ t ∈ [ 0 , τ ] : : t v ∈ D ( p B − p A , r A + r B ) } VO_{A|B}^{\tau} = \{v|\exists t \in [0,\tau]:: tv \in D(p_B - p_A,r_A + r_B)\} VOA∣Bτ={ v∣∃t∈[0,τ]::tv∈D(pB−pA,rA+rB)}
- V O A ∣ B τ VO_{A|B}^{\tau} VOA∣Bτ和 V O B ∣ A τ VO_{B|A}^{\tau} VOB∣Aτ关于原点对称

3.避免碰撞速度集合 C A A ∣ B τ ( V B ) CA_{A|B}^{\tau}(V_B) CAA∣Bτ(VB)(collision-avoiding velocities)
- 闵可夫斯基和 X ⨁ Y = x + y ∣ x ∈ X , y ∈ Y X \bigoplus Y = {x+y| x\in X,y\in Y} X⨁Y=x+y∣x∈X,y∈Y
- 如果 v b ∈ V B v_b \in V_B vb∈VB,那么 v A ∈ C A A ∣ B τ ( V B ) v_A \in CA_{A|B}^{\tau}(V_B) vA∈CAA∣Bτ(VB)时,在时间 τ \tau τ内AB不会碰撞 C A A ∣ B τ ( V B ) = { v ∣ v ∉ V O A ∣ B τ ⨁ V B } CA_{A|B}^{\tau}(V_B) = \{v|v \notin VO_{A|B}^{\tau} \bigoplus V_B\} CAA∣Bτ(VB)={ v∣v∈/VOA∣Bτ⨁VB}

4. 相互最大化(reciprocally maximal)
V A = C A A ∣ B τ ( V B ) V B = C A B ∣ A τ ( V A ) \begin{aligned} V_A = CA_{A|B}^{\tau}(V_B) \\ V_B = CA_{B|A}^{\tau}(V_A) \end{aligned} VA=CAA∣Bτ(VB)VB=CAB∣Aτ(VA)
5.ORCA(optimal reciprocal collision avoidance)
优化速度 v A o p t v_A^{opt} vAopt
(optimization velocities),为了定义ORCA引出的概念。- 虽然避免碰撞速度集合中有很多对速度 v A , v B v_A,v_B vA,vB,但希望选择出最接近优化速 v A o p t , v B o p t v_A^{opt},v_B^{opt} vAopt,vBopt的速度对
- 一般来说优化速度 v A o p t v_A^{opt} vAopt等于当前速度 v A v_A vA,这样机器尽可能少的偏离当前的轨道
ORCA几何定义

当 v A − v B ∈ V O A ∣ B τ v_A - v_B \in VO_{A|B}^{\tau} vA−vB∈VOA∣Bτ
- u u u是使点 v A − v B v_A - v_B vA−vB到速度障碍区 V O A ∣ B τ VO_{A|B}^{\tau} VOA∣Bτ边缘最近的点的向量。即使AB避免碰撞需要做的最小改变。
- n n n是该点的法向量
- AB都是可移动的机器,每人承担一半的避免碰撞的责任
- O R C A A ∣ B τ ORCA_{A|B}^{\tau} ORCAA∣Bτ是一个被直线分隔的半平面,这条直线通过点 v A o p t + 1 2 u v_A^{opt} + \frac{1}{2}u vAopt+21u,方向垂直于 n n n。
- O R C A B ∣ A τ ORCA_{B|A}^{\tau} ORCAB∣Aτ是一个被直线分隔的半平面,这条直线通过点 v B o p t − 1 2 u v_B^{opt} - \frac{1}{2}u vBopt−21u,方向垂直于 n n n。 O R C A A ∣ B τ = { v ∣ ( v − ( v A o p t + 1 2 u ) ) ⋅ n ≥ 0 } ORCA_{A|B}^{\tau} = \{v|(v - (v_A^{opt} + \frac{1}{2}u))\cdot n \geq 0\} ORCAA∣Bτ={ v∣(v−(vAopt+21u))⋅n≥0} ORCA定义
- O R C A A ∣ B τ ORCA_{A|B}^{\tau} ORCAA∣Bτ和 O R C A B ∣ A τ ORCA_{B|A}^{\tau} ORCAB∣Aτ互相避免碰撞和最大化 C A A ∣ B τ ( O R C A B ∣ A τ ) = O R C A A ∣ B τ C A B ∣ A τ ( O R C A A ∣ B τ ) = O R C A B ∣ A τ \begin{aligned} CA_{A|B}^{\tau}(ORCA_{B|A}^{\tau}) = ORCA_{A|B}^{\tau} \\ CA_{B|A}^{\tau}(ORCA_{A|B}^{\tau}) = ORCA_{B|A}^{\tau} \end{aligned} CAA∣Bτ(ORCAB∣Aτ)=ORCAA∣BτCAB∣Aτ(ORCAA∣Bτ)=ORCAB∣Aτ
- 并且 O R C A A ∣ B τ ORCA_{A|B}^{\tau} ORCAA∣Bτ和 O R C A B ∣ A τ ORCA_{B|A}^{\tau} ORCAB∣Aτ区域比其他的避免碰撞速度集合 V A ∈ C A A ∣ B τ ( V B ) , V B ∈ C A B ∣ A τ ( V A ) V_A \in CA_{A|B}^{\tau}(V_B),V_B \in CA_{B|A}^{\tau}(V_A) VA∈CAA∣Bτ(VB),VB∈CAB∣Aτ(VA)更接近 v A o p t , v B o p t v_A^{opt},v_B^{opt} vAopt,vBopt ∣ O R C A A ∣ B τ ⋂ D ( v A o p t , r ) ∣ = ∣ O R C A B ∣ A τ ⋂ D ( v B o p t , r ) ∣ ≥ min ( ∣ V A ⋂ D ( v A o p t , r ) ∣ , ∣ V B ∣ ⋂ D ( v B o p t , r ) ) \begin{aligned} |ORCA_{A|B}^{\tau} \bigcap D(v_A^{opt},r)| &= |ORCA_{B|A}^{\tau} \bigcap D(v_B^{opt},r)| \\ & \geq \min(|V_A \bigcap D(v_A^{opt},r)|,|V_B|\bigcap D(v_B^{opt},r)) \end{aligned} ∣ORCAA∣Bτ⋂D(vAopt,r)∣=∣ORCAB∣Aτ⋂D(vBopt,r)∣≥min(∣VA⋂D(vAopt,r)∣,∣VB∣⋂D(vBopt,r))
6.多个机器避免碰撞

O R C A A τ = D ( 0 , v A m a x ) ⋂ B ≠ A O R C A A ∣ B τ ORCA_A^{\tau} = D(0,v_A^{max}) \bigcap_{B\neq A}ORCA_{A|B}^{\tau} ORCAAτ=D(0,vAmax)B=A⋂ORCAA∣Bτ
再从线性规划出的区域中选择最接近首选速度 V A p r e f V_A^{pref} VApref的速度 v A n e w = arg min v ∈ O R C A A τ ∥ v − v A p r e f ∥ v_A^{new} = \arg \min_{v\in ORCA_A^{\tau} } \parallel v- v_A^{pref} \parallel vAnew=argv∈ORCAAτmin∥v−vApref∥- 这时都是在 v A o p t = v A v_A^{opt} = v_A vAopt=vA的基础上规划出的区域。也有可能规划出的区间为空 O R C A = ∅ ORCA=\empty ORCA=∅。如果选择合适的 v A o p t v_A^{opt} vAopt,ORCA永远不会是空,永远有解。并不明白
- 可以通过选择“附近”的机器,减少计算量(kd-tree寻找)
7.如何选择优化速度 v A o p t v_A^{opt} vAopt
- v A o p t = 0 v_A^{opt} = 0 vAopt=0

所有机器的优化速度为0时,保证 O R C A A τ ORCA_A^{\tau} ORCAAτ永远有解并不明白。但此时机器只考虑位置关系不考虑当前速度。机器密集时,也会导致死锁。
- v A o p t = v A p r e f v_A^{opt} = v_A^{pref} vAopt=vApref 当首选速度的值很大时,线性规划不可行,导航不安全。
- v A o p t = v A v_A^{opt} = v_A vAopt=vA 一个折中选择,优化速度会自适应。在低密度情况下会接近首选速度;高密度情况下会接近0.
8.高密度情况
- 如果 O R C A A τ = ∅ ORCA_A^{\tau}=\empty ORCAAτ=∅,不能保证 τ \tau τ时间内不会发生碰撞。这时选择一个“最安全的速度”.
- d A ∣ B ( v ) d_{A|B}(v) dA∣B(v)代表速度 v v v到 O R C A A ∣ B τ ORCA_{A|B}^{\tau} ORCAA∣Bτ的距离。(如果在平面范围内,值为负数)
- 使到所有平面的最大距离最小化 v A n e w = arg min v ∈ D ( 0 , v A m a x ) max B ≠ A d A ∣ B ( v ) v_A^{new} = \arg \min_{v\in D(0,v_A^{max})} \max_{B \neq A} d_{A|B}(v) vAnew=argv∈D(0,vAmax)minB=AmaxdA∣B(v)
9.静态障碍物
- 用线段 O O O表示静态障碍物
- 机器负责所有避障责任
- V O A ∣ O τ VO_{A|O}^{\tau} VOA∣Oτ由静态障碍物造成的速度障碍区 V O A ∣ O τ = { v ∣ ∃ t ∈ [ 0 , τ ] : t v ∈ O ⨁ } VO_{A|O}^{\tau} = \{v |\exists t\in[0,\tau]\::tv \in O \bigoplus \} VOA∣Oτ={ v∣∃t∈[0,τ]:tv∈O⨁}
- O R C A A ∣ O τ ORCA_{A|O}^{\tau} ORCAA∣Oτ是一个半平面,在A的速度 v A o p t v_A^{opt} vAopt距 V O A ∣ O τ VO_{A|O}^{\tau} VOA∣Oτ最近的点做切线,由切线分割平面
- 在遇到障碍物的时候,把所有机器的 v A o p t = 0 v_A^{opt}=0 vAopt=0,保证存在有效速度
- 同时,对于障碍物的时间 τ \tau τ可以更小

github上有代码,代码中处理静态障碍物时的 v A o p t v_A^{opt} vAopt并不是0.仍然是将A对障碍物的相对速度(其实就等于A的当前速度,因为静态障碍物没有速度)向 V O A ∣ B τ VO_{A|B}^{\tau} VOA∣Bτ的边缘最近的点做垂线,并在垂点做切线,这条切线就是A的 O R C A A ∣ B τ ORCA_{A|B}^{\tau} ORCAA∣Bτ(因为静态障碍物没有速度,所有避免碰撞做需要做出的改变 u u u都需要机器A负责,而 v A + u v_A+u vA+u就是垂点,因此 O R C A A ∣ B τ ORCA_{A|B}^{\tau} ORCAA∣Bτ就是通过此点的切线)。